Nmap is the most popular free security scanner developed by Gordon Lyon (f.f. Fyodor Vaskovich). The first version of Nmapa was published on October 1, 1997, in the online magazine, Phrack.
For those interested in the beginnings of this scanner, here is a full article that shows the capabilities and source code of the first version of Nmap: The Art of Port Scanning.
At the time of writing this text, the latest version of Nmap is 7.70. This version is equipped with 588 NSM scripts (Nmap Scripting Engine), which, along with a huge number of standard scanning options, give the opportunity to examine more carefully the hosts we are interested in.
NSE can be used, among others, to more accurately detect the version of a given service, break usernames and passwords, detect and use known vulnerabilities, and even detect existing back gates left by the attacker and fuzzing.
A list of all available scripts with descriptions is published at https://nmap.org/nsedoc/. Alternatively, to get a list, we can use the terminal (assuming that Nmap has been installed in the default location):
LINUX
- ls -1 /usr/share/nmap/scripts
WINDOWS
- dir “C:\Program Files\Nmap\scripts”
or
- dir “C:\Program Files (x86)\Nmap\scripts”
To obtain information on the purpose of the script, use the command:
- nmap –script-help <nazwa_skryptu>
Below, I will try to present some useful NSE scripts from the perspective of pentesters and scripts administrators.
1. http-enum.nse
The http-enum script, using the default fingerprints database, sends over 2,000 queries to the web server, trying to reach files and/or directories specific to popular web applications. If the server returns the code “200 OK” or “401 Authentication Required” to any of the queries, it will mean that the desired file or directory is available on the server, and then the fingerprint script will return the name of the application.
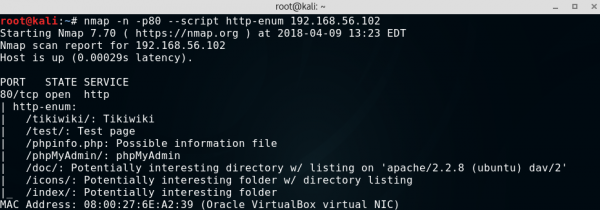
The operation of this script is similar to the operation of the popular Web application Scanner – Nikto, and it is possible to connect the Nikto fingerprint database, containing more than 6,500 entries, to the default script database using the argument http-fingerprints.nikto-db-path. If, after this argument, we do not provide the path to the Nikto database, the script will try to locate the db_tests database itself.
Alternatively, we can create our own database of fingerprints and indicate it in the http-enum.fingerprintfile argument. To do this, create a script in Lua, for example, with the following content:
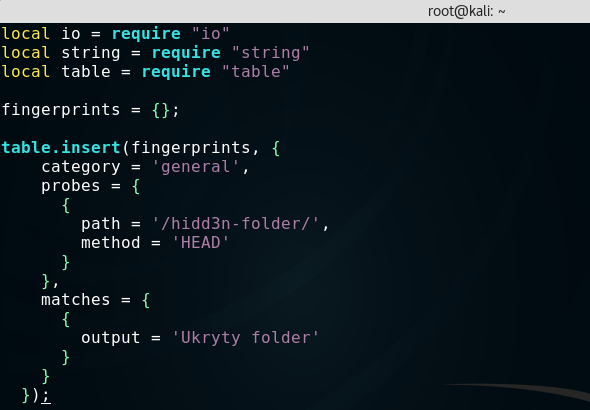
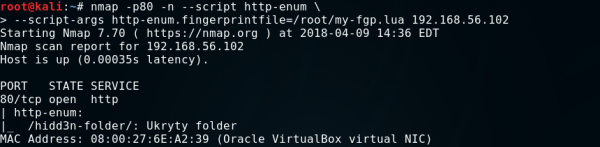
Next, we indicate the path to the script in the http-enum.fingerprintfile argument.
Another useful argument is http-enum.basepath, which takes the path from which the scan will start as a parameter.
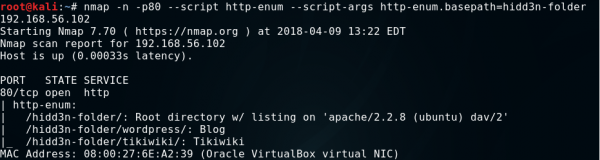
By default, the http-enum script treats those files and folders as existing , to which the server responds with the codes “200 OK” and “401 Authentication Required.” To extend this scope to all codes (except “404 Not Found“), use the http-enum.displayall argument. As a result, the probability of finding hidden folders is higher, but much more false-positives are generated.
2. http-grep.nse
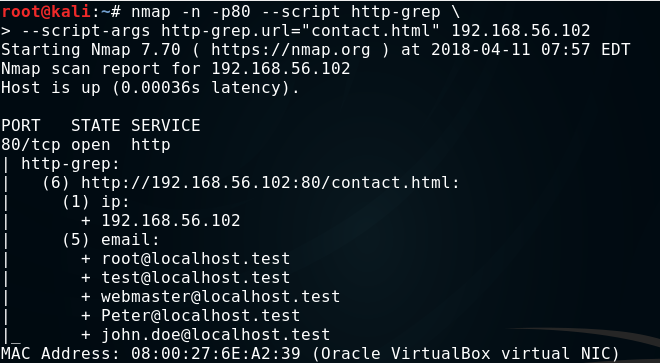
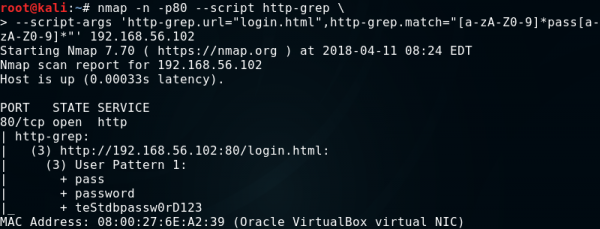
The http-grep script searches the given page for useful information. By default, it returns the e-mail addresses and IP addresses found on all subpages discovered by the script. We can give the script in the http-grep.url argument subpage that we want to search, and using the argument, http-grep.builtins, we will extend the scope of the search to email addresses, IP addresses, phone numbers, mastercard, visa, discover, amex, and ssn cards. If we want to add a word or regular expression to be searched, we pass it to the argument, http-grep.match. By default, set to 3, the search depth can be changed using the http-grep.maxdepth argument.
3. ssh-brute.nse
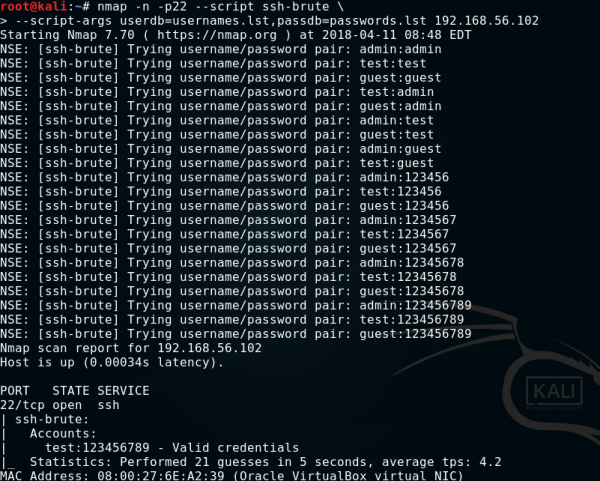
The ssh-brute script is used to break SSH service passwords with predictive text input. By default, it uses its own database, rather an extensive database of users and passwords. However, you can pass our letters to the script using the userdb and passdb arguments.
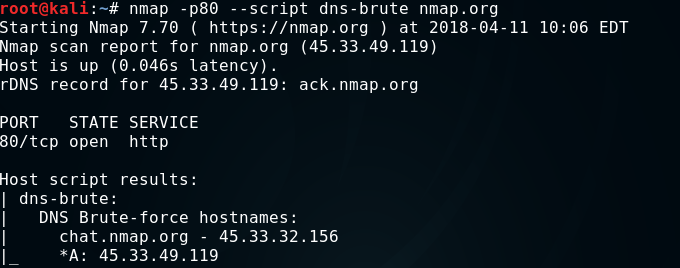
4. dns-brute.nse
The dns-brute script tries to find as many subdomains as the host is being tested using the most frequently used subdomain names.
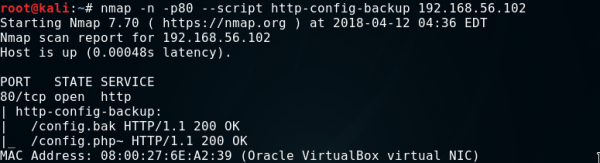
5. http-config-backup.nse
The http-config-backup script sends many queries to the web server, trying to get a copy of the configuration of popular CMS left behind by the user or text editor. According to the research conducted by the author of the CMSploit tool, which is inspired by the http-config-backup script, almost 1% of websites using CMS reveal their access data to the database through left copies of the configuration.
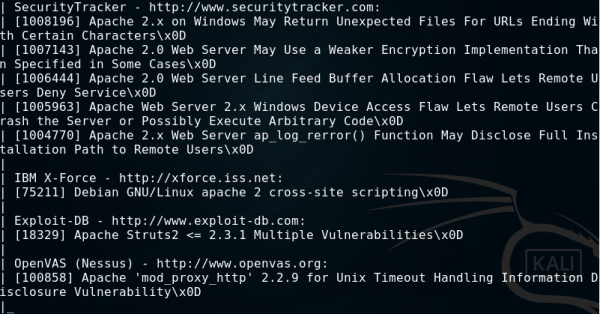
6. vulscan.nse
The vulscan script adds Nmap’s vulnerability scanner functionality. Unfortunately, it is not part of the standard Nmap script library, so to use it, please download it from http://www.computec.ch/projekte/vulscan/?s=download and place the unpacked vulscan folder in the Nmap scripts directory.
In case of this script, you must use the additional option -sV, which is used to detect the version of the scanned software, and then, on its basis, the script using several databases (.csv files in the vulscan folder) suggests possible vulnerabilities.

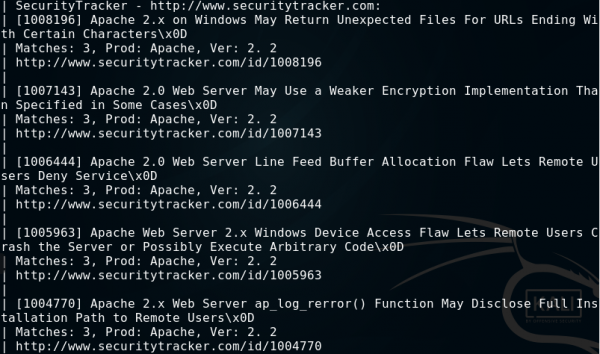
To change the script result template, you can use the vulscanoutput argument, which can take one of four arguments:
- details – as a result, we will get the name of the vulnerability, the number of matches, the name and version of the software, and links to exploits or vulnerability explanations
- listid – as a result, we get the same ID or CVE detected vulnerabilities
- listlink – as a result, we will get links to exploits or vulnerabilities
- listtitle – as a result, we will only get the names of detected vulnerabilities
You can also create your own template with the help of the following elements:
- {id} – vulnerability ID
- {title} – vulnerability title
- {matches} – the number of matches
- {product} – the name of the software
- {version} – software version
- {link} – link to exploit/explanation of vulnerability
- \n – a new line
- \t – tabulator
This is what the command will look like, the result of which is to be a table containing the ID and the vulnerability link:
|
1 |
nmap -sV --script vulscan/vulscan --script-args vulscanoutput='{id}\t{link}' |
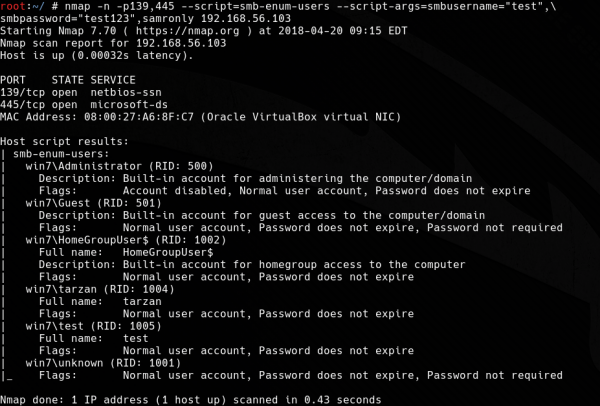
7. smb-enum-users.nse
The task of the smb-enum-users script is to enumerate all users available on the scanned Windows system. This script uses the MSRPC (Microsoft RPC) protocol and two enumeration techniques:
- SAMR – this technique returns more information than the user’s name itself, is much less “noisy” than LSA, and because it uses a dedicated function, it will return all existing accounts. Requires minimum user privileges (does not require any permissions on Windows 2000);
- LSA – in addition to usernames, returns system accounts, groups, and aliases. Requires less authorization from SAMR – it can be used with guest privileges, but it generates a large number of logs on the scanned system.
When we run the script without arguments, it will use both of the above techniques. If you want to limit scanning to one technique, just use the argument:
- samronly – for SAMR-only scanning;
- lsaonly – for scanning only by LSA.
If a guest account with an empty password is not available on the scanned system, we will have to use the smsusername and smbpassword arguments and give the system user access data. In this case, you can also limit the scan to the SAMR technique itself to make it “quieter.”
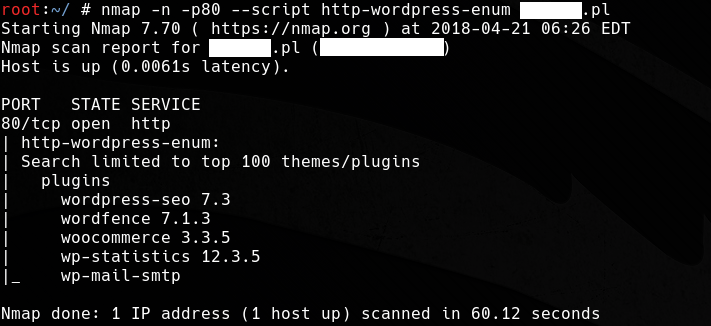
8. http-wordpress-enum.nse
The http-wordpress-enum script, using the wp-themes.lst database containing about 32 thousand entries and the wp-plugins.lst database with over 14,000 WordPress plugins, checks which themes and plugins have been installed on the scanned site. The names in the databases are sorted by popularity. Passing a number in the http-wordpress-enum.search-limit argument will change the default value of checking for the 100 most popular plugins and themes, and when we pass “all,” all names from the databases will be checked. If WordPress on the tested server has been installed in a non-standard directory, we indicate its path in the http-wordpress-enum.root argument. Another useful parameter is http-wordpress-enum.check-latest, which will check the validity of the plugins and motives if we pass “true.“
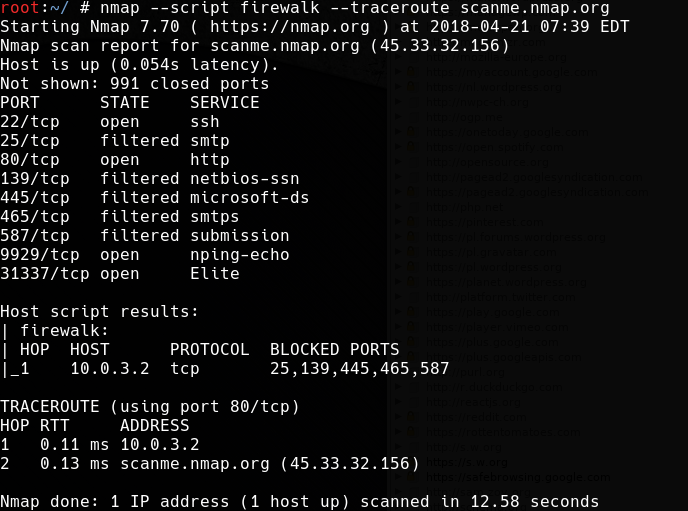
9. firewalk.nse
Firewalk script, using the package tracking technique (traceroute) and the passage of TTL, known as firewalking, attempts to detect firewall/gateway rules. The scanning parameters can be controlled using the following arguments:
- firewalk.max-probed-ports – the number of ports to be tested for each protocol. Set to -1, examine all filtered ports;
- firewalk.max-retries – the maximum amount of retransmissions;
- firewalk.recv-timeout – the duration of the loop that collects packets (in milliseconds);
- firewalk.max-active-probes – maximum number of parallel scans;
- firewalk.probe-timeout – validity of a single scan (in milliseconds).
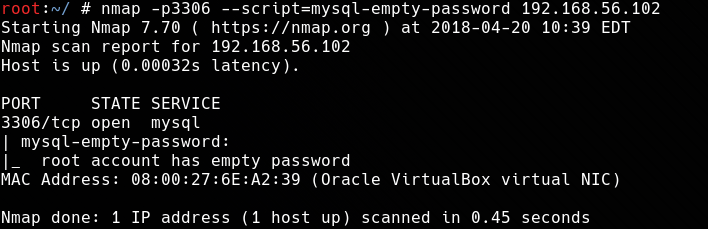
10. mysql-empty-password.nse
The mysql-empty-password script checks whether it is possible to log in to the MySQL server to the root or anonymous account using an empty password.
11. mysql-users.nse
The mysql-users script is used to list the users available on the MySQL server. To list, we will use the root account with an empty password, which we discovered in the previous script. We provide access data in the mysqluser and mysqlpass arguments. When the password is empty, you can omit the mysqlpass argument.

12. mysql-brute.nse
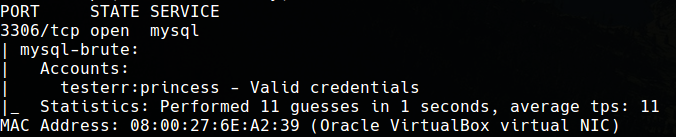
The mysql-brute script is used to break access data to the MySQL server. The previous script has detected the user testerr whose password we will now try to break. In the beginning, create a file with usernames; in this example, it will only be a testerr user.

Next, we pass the created list to the userdb argument, and, optionally, we can use the passdb argument to indicate the password database.
It is not necessary to give your scripts to your database, and if you do not do it, it will use default databases with the most popular logins and passwords. In this example, we’ll use the default database of over 5,000 popular passwords without using the passdb argument.
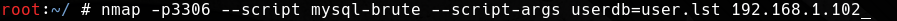
Summary
Nmap should undoubtedly be one of the basic tools of every pentester and administrator, and the ever-growing number of extensive NSE scripts makes it having the features that allow detailed testing of network security without the need to use other tools.