Calculation of pseudo-random numbers generator state – on the example of Math. random() from Firefox

In this text:

We will get to know how pseudo-random number generators operate
We will learn how the XorShift128Plus algorithm, which is the basis of pseudo-random number generators in all the most popular browsers (Firefox, Chrome, Edge), works.
We will get to know the Z3Prover tool, thanks to which we will be able to calculate the state of the generator on the basis of three known numbers.

In real cases, knowing the status of a random number generator may allow, for example, to guess subsequent session tokens.

Inspiration

The direct inspiration for writing this article was from a random4 task with a very interesting set of challenges called return true to win puzzles. Each task contains a short piece of code with a defined function that returns a Boolean value. The task of the solver is to pass such parameters to the function so that it returns “true”. This is not always easy. Usually, it requires knowledge of the nuances of the ECMAScript standard or, going even further, the specific features of JavaScript in browsers. I recommend that you try to face these tasks because they allow you to learn more about the most relevant programming language of the web world. But let’s go back to random4. The code was as follows:

var rand = Math.random();
function random4(x) {
  return rand === x;
}

var rand = Math.random();

function random4(x) {

return rand === x;

}

As we can see, a random value generated by Math.random() is assigned to the rand variable. In the next step, we have to call the random4 function with such a parameter that it returns true. In other words, our parameter must be equal to the previous value of Math.random()… Once all the ideas failed and it seemed that no specific feature of Javascript (or browser error) was at stake here, the task came down to another problem: You have to determine the state of the pseudo-random generator!

How do pseudo-random number generators work

Apart from cryptographic applications, where a lot of attention is paid to the fact that random numbers are, in fact, random, in other areas we usually deal with pseudo-random numbers. The methods of generating pseudo-random numbers are different – depending on the algorithm we use – but basically come down to a few steps:

We pass the seed to the generator of pseudo-random numbers. This way, the state of the generator is determined by the seed.
The generator performs arithmetic operations, on the basis of which it calculates the new state value.
On the basis of the generator state, a new pseudo-random value is calculated.

A characteristic feature of pseudo-random number generators is that when the same seed is used, one will receive the exact same sequence of numbers.

Repeatability of pseudo-random generators in the same state is a desirable feature because it allows to re-create the workflow of the program, e.g., in case of an error.

Pseudo-random number generators in web browsers

All the most popular web browsers (i.e. Chrome, Firefox, and Edge) use the same algorithm to generate pseudo-random numbers: XorShift128+. In the next part of the text, however, I will refer only to the implementation from Firefox, due to the fact that in my opinion, it is the most readable.

So let’s see the appropriate fragment of the code from the Gecko engine:

XorShift128PlusRNG(uint64_t aInitial0, uint64_t aInitial1) {
  setState(aInitial0, aInitial1);
}
 
uint64_t next() {
  uint64_t s1 = mState[0];
  const uint64_t s0 = mState[1];
  mState[0] = s0;
  s1 ^= s1 << 23; mState[1] = s1 ^ s0 ^ (s1 >> 17) ^ (s0 >> 26);
  return mState[1] + s0;
}

XorShift128PlusRNG(uint64_t aInitial0, uint64_t aInitial1) {

setState(aInitial0, aInitial1);

}

uint64_t next() {

uint64_t s1 = mState[0];

const uint64_t s0 = mState[1];

mState[0] = s0;

s1 ^= s1 << 23; mState[1] = s1 ^ s0 ^ (s1 >> 17) ^ (s0 >> 26);

return mState[1] + s0;

}

As you can see in the code above, the state of the XorShift128+ generator consists of two 64-bit numbers. The next pseudo-random number is calculated by converting the new value of one of the state numbers (which can be achieved by several bit shifts and XOR operations), and then adding two state numbers to each other.

Insightful readers will notice that XorShift128+ generates 64-bit integers, while Math.random() returns a floating point number in the [0, 1) range. So how is this uint64_t converted to double? This question is answered by another function from the sources: nextDouble.

double nextDouble() {
  static constexpr int kMantissaBits =
mozilla::FloatingPoint::kExponentShift + 1;
  uint64_t mantissa = next() & ((UINT64_C(1) << kMantissaBits) - 1);
  return double(mantissa) / (UINT64_C(1) << kMantissaBits);
}

double nextDouble() {

static constexpr int kMantissaBits =

mozilla::FloatingPoint::kExponentShift + 1;

uint64_t mantissa = next() & ((UINT64_C(1) << kMantissaBits) - 1);

return double(mantissa) / (UINT64_C(1) << kMantissaBits);

}

The code boils down to the fact that from the generated 64-bit value 53 last bits are taken, which are then divided by 2⁵³. In this way we have a guarantee that we will get a number from the range [0,1). It did not make sense to divide more bits because the double data type is not able to hold more precision anyway.

While all the most popular browsers use the XorShift128+ algorithm, each of them has its own way to convert unit64_t to double. Therefore, the code we will write for Firefox will not be compatible with other browsers, although it will require only minor corrections.

As a simple exercise, which is the basis for our further operations, let’s rewrite the code generating pseudo-random numbers to Python.

class XorShift128PlusFirefox(object):
    def __init__(self, s0, s1):
        self.s0 = s0
        self.s1 = s1
        self.state = [s0, s1]
        
    def next(self):
        s1 = self.state[0]
        s0 = self.state[1]
        
        self.state[0] = s0
        s1 ^= (s1 << 23)
        s1 &= 0xffffffffffffffffL
        self.state[1] = s1 ^ s0 ^ (s1>>17) ^ (s0>>26)
                
        random_val = (self.state[1] + s0) & 0xffffffffffffffffL 
        
        return random_val
    
    def next_double(self):
        return float(self.next() & 0x1fffffffffffffL) / 2**53

class XorShift128PlusFirefox(object):

def __init__(self, s0, s1):

self.s0 = s0

self.s1 = s1

self.state = [s0, s1]

def next(self):

s1 = self.state[0]

s0 = self.state[1]

self.state[0] = s0

s1 ^= (s1 << 23)

s1 &= 0xffffffffffffffffL

self.state[1] = s1 ^ s0 ^ (s1>>17) ^ (s0>>26)

random_val = (self.state[1] + s0) & 0xffffffffffffffffL

return random_val

def next_double(self):

return float(self.next() & 0x1fffffffffffffL) / 2**53

The above code is practically a literal translation of the C++ code into Python. The XorShift128PlusFirefox class in the constructor has two values defining the state of the generator; next() function generates another 64-bit integer, and next_double() generates another floating point-type number in the range [0,1).

In the code of the next_double() function we see the use of Python function float(). Only one floating-point type is defined in Python. It corresponds to the double type known from C/C++, but is called float.

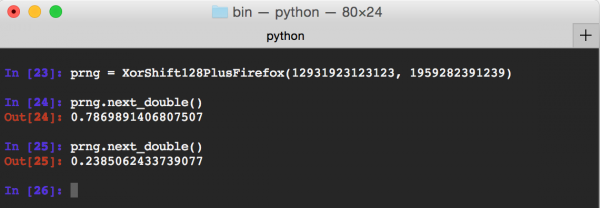
An example of using XorShift128PlusFirefox class can be seen in Picture nr 1. Two pseudo-random numbers were generated based on the given state.

picture nr 1 Generation of two random numbers with the XorShift128+ algorithm

Z3Prover tool

We already know how the random number generator works in Firefox; we even wrote its implementation in Python. We are slowly approaching the essence of this text, i.e., the determination of the generator’s state based on the knowledge of a few numbers. But let’s get to know the tool we can use to achieve this: Z3Prover. Z3Prover is a SMT solver class tool – it allows for automatic proving of theorems. In short, the tool accepts as an input a set of logical conditions (which may consist of arithmetic and bit operations, among others), and then tries to calculate whether there is input data for which these conditions are met. A few examples we will see below.

To start using Z3Prover, you must first compile its sources or download binary files. I recommend using the second option. After unpacking the binary files, run Python in the same directory in which they were unpacked and call the command:

from z3 import *
# or alternatively
import z3

from z3 import *

# or alternatively

import z3

Example 1

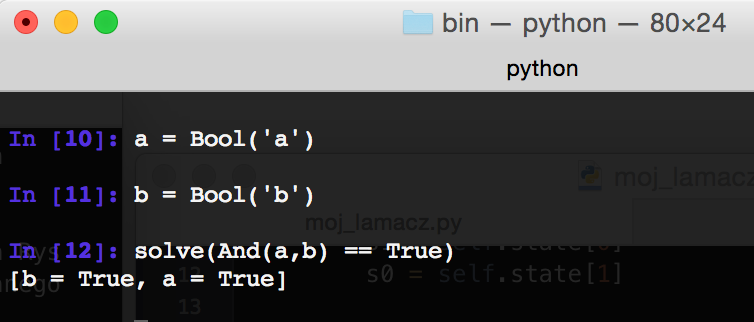
We start with a trivial example: We define two symbols, which are Boolean variables, and check when their conjunction will be equal to the ”ture”. Of course, z3 returns to us the answer that the equation is fulfilled when both variables are true.

Example 2

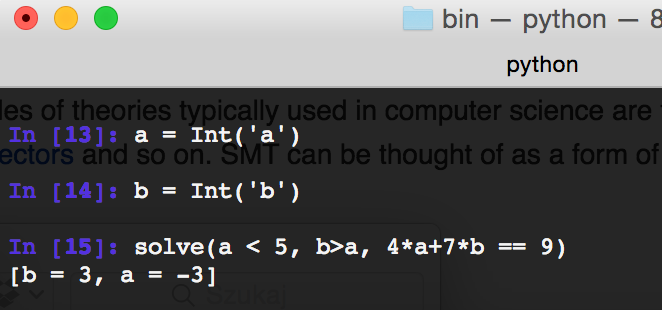
In z3 we can also operate on numbers. In this example, we have defined two integers, and then we try to solve the equation: 4*a+7*b=9 with the assumption that a<5 and b>a.

picture nr 3 Operating on integers in z3

Example 3

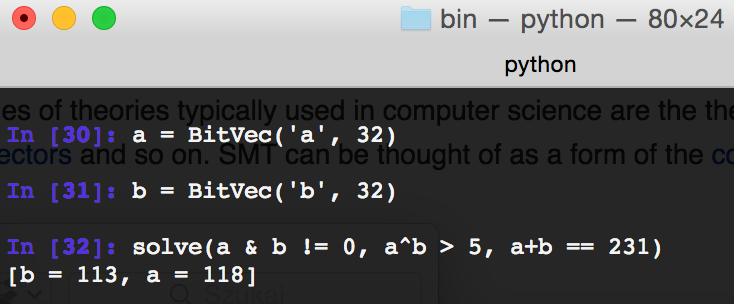
Another type of data we learn is BitVec – it is an integer with the number of bits we have set. Then we try to solve an equation in which we combine both bit and arithmetic operators.

picture nr 4 Operating on numbers with particular bit number

Example 4

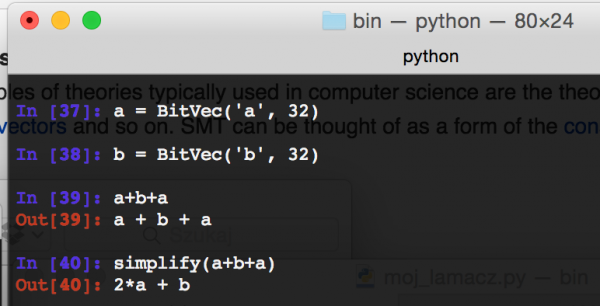
Z3 can also be used to simplify certain symbolic expressions instead of calculating them.

picture nr 5 Using z3 to simplify expressions

“Cracking” number generator

It’s time to write a “cracker” for the random number generator, which works well for a few elements:

Using z3 we will save a symbolic figure of three consecutive random numbers generated by the XorShift128+ algorithm,
Three consecutive floating point numbers generated by Math.random() will be changed to integers,
Based on the above data, we will generate three equations with variables s0 and s1, the solution of which will allow us to determine the state of the generator of pseudo-random numbers.

Let us start with basic definitions:

class Cracker(object):
    def __init__(self, known_values):
        # state variables are two 64-bit numbers
        self.s0 = z3.BitVec('s0', 64)
        self.s1 = z3.BitVec('s1', 64)
        self.state = [self.s0, self.s1]
        
        # Solver class is a class to which we can add
        # equations that we will want to solve in the long run
        self.solver = z3.Solver()
        
        # the known variable will contain known values
        # pseudo-random numbers generated in Firefox
        self.known = known_values

class Cracker(object):

def __init__(self, known_values):

# state variables are two 64-bit numbers

self.s0 = z3.BitVec('s0', 64)

self.s1 = z3.BitVec('s1', 64)

self.state = [self.s0, self.s1]

# Solver class is a class to which we can add

# equations that we will want to solve in the long run

self.solver = z3.Solver()

# the known variable will contain known values

# pseudo-random numbers generated in Firefox

self.known = known_values

We have the Cracker class, in which we define the variables s0 and s1 containing the generator state and the state variable containing the same, but in the form of an array. Field solver stores the Solver class of z3, which takes the equations to solve. To known field we will pass known values of pseudo-random numbers, which we will generate using Math.random() method from Firefox.

So let’s implement the next() generator method:

def next(self):
        s1 = self.state[0]
        s0 = self.state[1]
        
        self.state[0] = s0
        s1 ^= (s1 << 23)
        self.state[1] = s1 ^ s0 ^ z3.LShR(s1,17) ^ z3.LShR(s0,26)
                
        return self.state[1] + s0

def next(self):

s1 = self.state[0]

s0 = self.state[1]

self.state[0] = s0

s1 ^= (s1 << 23)

self.state[1] = s1 ^ s0 ^ z3.LShR(s1,17) ^ z3.LShR(s0,26)

return self.state[1] + s0

The next() method looks exactly the same as in the original Firefox code. The only difference is the use of z3.LShR instead of operator >>. This is due to the fact that in z3 the operator >> is an arithmetic bit shift to the right. Consequently, if the character bit is 1, it will be retained. LShR is a logical right shift that ensures that the sign bit will always be set to 0. Let’s see, out of curiosity, what random numbers look like in a symbolic form after the first two calls to the next() function (Picture nr 6).

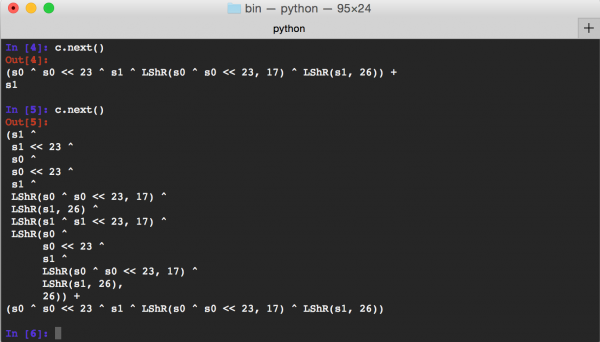
picture nr 6 The first two calls of next() in symbolic form

After the first next() call, the symbolic form is almost exactly the same as we saw in the code of this method. After the second call, the situation starts to get more complicated; we can see a more complicated description of the number, although the only variables to which it refers are s0 and s1.

Now we will generate three random numbers in Firefox:

The first random number will be equal to the symbolic number form after the first call to next(),
The second random number will be equal to the form of the symbolic number after the second call to next(),
The third random number will be equal to the symbolic number form after the third call to next().

We have one important problem to solve: next() function returns a number in the form of uint64_t, and from Firefox we will get floating-point numbers. We will therefore have to convert it back into integers. However, this will not be difficult. As we remember, Firefox pulled out of the 64-bit number its 53 last bits, and then divided it by 2⁵³. So we will simply reverse this process. The number we get from Firefox will be multiplied by 2⁵³, and from the number we have in a symbolic form, we will extract only 53 bits. As a result, we get two 53-bit integers to compare. Let’s look at the code of the “cracker” itself:

def crack(self):
        for val in self.known:
            self.solver.add((self.next() & 0x1fffffffffffff) == long(val * 2**53))
        if self.solver.check() != z3.sat:
            raise("Not solved!")
        
        model = self.solver.model()
        s0 = model[self.s0].as_long()
        s1 = model[self.s1].as_long()
        
        return (s0, s1)

def crack(self):

for val in self.known:

self.solver.add((self.next() & 0x1fffffffffffff) == long(val * 2**53))

if self.solver.check() != z3.sat:

raise("Not solved!")

model = self.solver.model()

s0 = model[self.s0].as_long()

s1 = model[self.s1].as_long()

return (s0, s1)

In the above code we iterate after known values of random numbers. Multiply the values of the double type by 2⁵³ and compare them with the 53 last bits of the number generated by calling next(). Such equations are thrown into the solver with z3. Then we call the solver. check() method solving the equations given by us. If the method returns the value of z3. sat, it means that the equation has been solved. The calculated values can be extracted by referring to the model. Finally, the function returns s0 and s1, which are the state of the random number generator.

So I generated three consecutive random numbers in Firefox:

0.8629073810129263,
0.19187870241845773,
0.07371019627869657.

Let’s see if our Cracker will be able to determine the state of the generator (Picture nr 7)

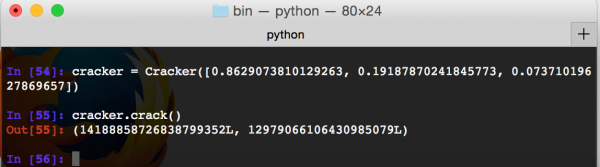
picture nr 7 Determining the state of generator based on three numbers

Success! Thanks to z3 we reconstructed the generator’s state. Now let’s try to use this state as an argument to the generator we wrote earlier (class XorShift128PlusFirefox) and see if it really will generate the same numbers (Picture nr 8).

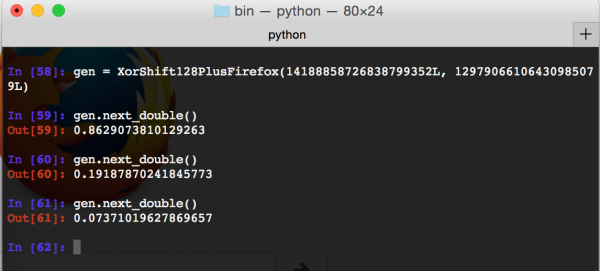
picture nr 8 Using the calculated state to generate numbers again

We got the same sequence that Firefox generated, which shows that our Python implementation of breaking and generating further pseudo-random numbers is correct.

Solving problem from random4 task

The problem with the random4 task mentioned at the beginning remains to be solved. Due to the specificity of that task, we could generate as many random numbers as we wanted, but we had to determine what number was generated before our Math.random() calls. It turns out that with the current code the solution to such a problem is easy: After calculating the generator state, we will not call the next() method (it causes the calculation of a new state), but we will generate a number on the basis of the state that we know.

Below is the full code of the solution – the changes described in the paragraph above are reflected in the current_double() method. In addition, a code has been added to the Python script to pass an argument containing three comma-separated numbers generated in Math.random().

# -*- coding: utf-8 -*-
import z3
import sys
 
class XorShift128PlusFirefox(object):
    def __init__(self, s0, s1):
        self.s0 = s0
        self.s1 = s1
        self.state = [s0, s1]
    
    def current_double(self):
        val = (self.s0 + self.s1) & 0x1fffffffffffffL
        return float(val) / 2**53
    
    def next(self):
        s1 = self.state[0]
        s0 = self.state[1]
        
        self.state[0] = s0
        s1 ^= (s1 << 23)
        s1 &= 0xffffffffffffffffL
        self.state[1] = s1 ^ s0 ^ (s1>>17) ^ (s0>>26)
                
        random_val = (self.state[1] + s0) & 0xffffffffffffffffL 
        
        return random_val
    
    def next_double(self):
        return float(self.next() & 0x1fffffffffffffL) / 2**53
    
class Cracker(object):
    def __init__(self, known_values):
        # State variables are two 64-bit numbers.
        self.s0 = z3.BitVec('s0', 64)
        self.s1 = z3.BitVec('s1', 64)
        self.state = [self.s0, self.s1]
 
        # Solver class is a class to which we can add
        # equations that we will want to solve in the long run
        self.solver = z3.Solver()
 
        # The known variable will contain known values of
        # pseudo-random numbers generated in Firefox.
        self.known = known_values
    
    def next(self):
        s1 = self.state[0]
        s0 = self.state[1]
        
        self.state[0] = s0
        s1 ^= (s1 << 23)
        self.state[1] = s1 ^ s0 ^ z3.LShR(s1,17) ^ z3.LShR(s0,26)
                
        return self.state[1] + s0
    
    def crack(self):
        # Because of the way numbers are generated in Firefox,
        # from the number calculated by 3 we take only the youngest 53
        # Bits. In turn the floating-point number should be replaced by the following
        # integers by multiplying it by 2**53.
        for val in self.known:
            self.solver.add((self.next() & 0x1fffffffffffff) == long(val * 2**53))
        if self.solver.check() != z3.sat:
            raise Exception("Not solved!")
        
        model = self.solver.model()
        s0 = model[self.s0].as_long()
        s1 = model[self.s1].as_long()
        
        return (s0, s1)
 
def main():
    # Take one argument from the command line representing
    # several floating-point numbers separated by commas.
    known_values = [float(v) for v in sys.argv[1].split(",")]
    
    # We „break” the state of the random number generator.
    cracker = Cracker(known_values)
    (s0, s1) = cracker.crack()
    
    # We use the calculated generator state to calculate
    # the previous pseudo-random number.
    prng = XorShift128PlusFirefox(s0, s1)
    print "{:.16}".format(prng.current_double())
 
if __name__ == '__main__':
    main()

# -*- coding: utf-8 -*-

import z3

import sys

class XorShift128PlusFirefox(object):

def __init__(self, s0, s1):

self.s0 = s0

self.s1 = s1

self.state = [s0, s1]

def current_double(self):

val = (self.s0 + self.s1) & 0x1fffffffffffffL

return float(val) / 2**53

def next(self):

s1 = self.state[0]

s0 = self.state[1]

self.state[0] = s0

s1 ^= (s1 << 23)

s1 &= 0xffffffffffffffffL

self.state[1] = s1 ^ s0 ^ (s1>>17) ^ (s0>>26)

random_val = (self.state[1] + s0) & 0xffffffffffffffffL

return random_val

def next_double(self):

return float(self.next() & 0x1fffffffffffffL) / 2**53

class Cracker(object):

def __init__(self, known_values):

# State variables are two 64-bit numbers.

self.s0 = z3.BitVec('s0', 64)

self.s1 = z3.BitVec('s1', 64)

self.state = [self.s0, self.s1]

# Solver class is a class to which we can add

# equations that we will want to solve in the long run

self.solver = z3.Solver()

# The known variable will contain known values of

# pseudo-random numbers generated in Firefox.

self.known = known_values

def next(self):

s1 = self.state[0]

s0 = self.state[1]

self.state[0] = s0

s1 ^= (s1 << 23)

self.state[1] = s1 ^ s0 ^ z3.LShR(s1,17) ^ z3.LShR(s0,26)

return self.state[1] + s0

def crack(self):

# Because of the way numbers are generated in Firefox,

# from the number calculated by 3 we take only the youngest 53

# Bits. In turn the floating-point number should be replaced by the following

# integers by multiplying it by 2**53.

for val in self.known:

self.solver.add((self.next() & 0x1fffffffffffff) == long(val * 2**53))

if self.solver.check() != z3.sat:

raise Exception("Not solved!")

model = self.solver.model()

s0 = model[self.s0].as_long()

s1 = model[self.s1].as_long()

return (s0, s1)

def main():

# Take one argument from the command line representing

# several floating-point numbers separated by commas.

known_values = [float(v) for v in sys.argv[1].split(",")]

# We „break” the state of the random number generator.

cracker = Cracker(known_values)

(s0, s1) = cracker.crack()

# We use the calculated generator state to calculate

# the previous pseudo-random number.

prng = XorShift128PlusFirefox(s0, s1)

print "{:.16}".format(prng.current_double())

if __name__ == '__main__':

main()

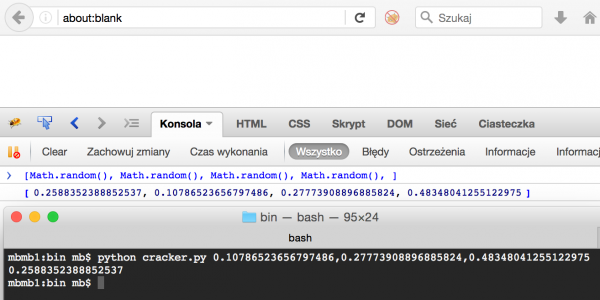
As a final test of the correctness of the solution, I will generate four more pseudo-random numbers in Firefox, pass the last three to the cracker, and see if the first one will be generated (Picture nr 9).

Summary

In all popular web browsers today, the generation of pseudo-random numbers takes place using the XorShift128+ algorithm. Generating consecutive numbers consists of performing a few simple arithmetic and logical operations, and thus knowing a few consecutive numbers, we can determine the state of the generator, which will allow both the conversion of what numbers will be generated next, as well as the determination of numbers generated earlier. The article shows how to use the z3 tool to determine the state of the generator, which is allowed to “guess” what pseudo-random number was generated in Firefox before the three numbers given as an argument to the program.

The article also shows that the Math.random() method should not be used in cryptographic applications. In JavaScript, the getRandomValues() method should be used for cryptographic purposes.

Tagged: Mozilla Firefox, pseudo-random